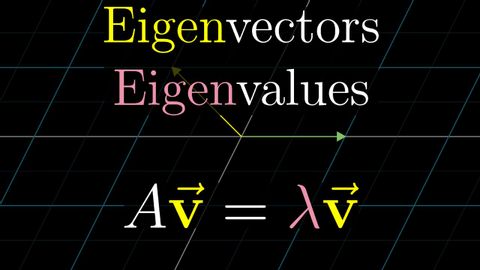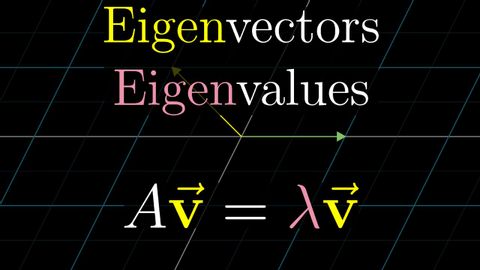字幕リスト動画再生

    動画が英語ではありませんか？
    字幕と単語

    00
    保存
    動画の中の単語

    stretch

    US /strɛtʃ/

    ・

    UK /stretʃ/

    • v.t./i.ストレッチをする : 体を伸ばす；伸ばす : 張る : 広げる
    • n.ストレッチ : 体を伸ばすこと；一続きのもの；(一続きの)時間 : 期間
    A2 初級TOEIC
    もっと見る
    expression

    US /ɪkˈsprɛʃən/

    ・

    UK /ɪk'spreʃn/

    • n. (c./u.)表現；語句；表情；式；表現；表現
    A2 初級TOEIC
    もっと見る
    scale

    US /skel/

    ・

    UK /skeɪl/

    • n. (c./u.)大きさや格など；うろこ；はかり；音階；規模
    • v.t./i.(縮尺比に従って)拡大する : 縮小する；登る；魚のうろこを取る
    A2 初級TOEIC
    もっと見る
    spot

    US /spɑt/

    ・

    UK /spɒt/

    • n.地点 : 場所；困難 : 苦境；位置づけ；少し；斑点 : 染み : 汚点
    • v.t.(偶然)見つける
    A2 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary