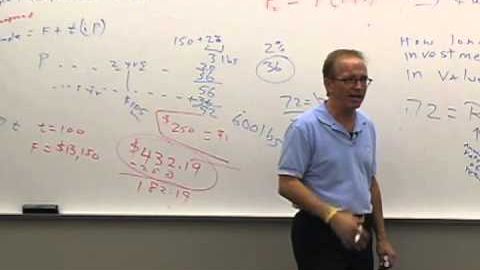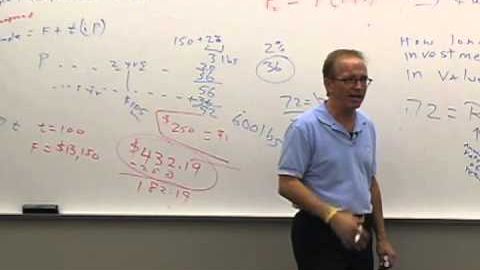字幕リスト動画再生

    字幕と単語

    00
    保存
    動画の中の単語

    present

    US /ˈprɛznt/

    ・

    UK /'preznt/

    • adj.出席している；現在
    • n.プレゼント；現在時制；現在；贈り物
    • v.t.紹介する；司会をする；発表する；提示する；(賞を)贈呈する
    • v.i.現れる
    A1 初級TOEIC
    もっと見る
    term

    US /tɚm/

    ・

    UK /tɜ:m/

    • n. (c./u.)条件；期間；学期；用語；関係；項；妊娠期間；任期
    • v.t.称する
    A1 初級TOEIC
    もっと見る
    general

    US /ˈdʒɛnərəl/

    ・

    UK /'dʒenrəl/

    • adj.一般的な；大まかな；広範囲に適用できる；総司令官の
    • n. (c.)大将
    • n. (c./u.)一般大衆；一般的な研究分野
    A1 初級TOEIC
    もっと見る
    exact

    US /ɪɡˈzækt/

    ・

    UK /ɪɡ'zækt/

    • adj.正確な : 精密な
    • v.t.(力ずくで)～を取り立てる : (強制的に)～を取り出す
    A2 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary