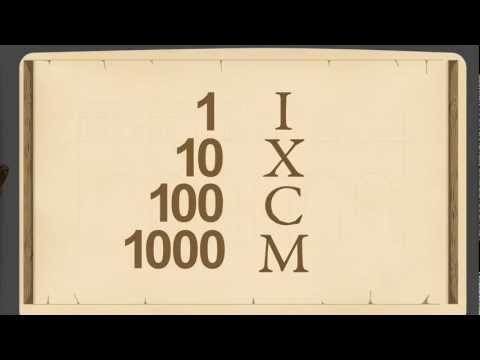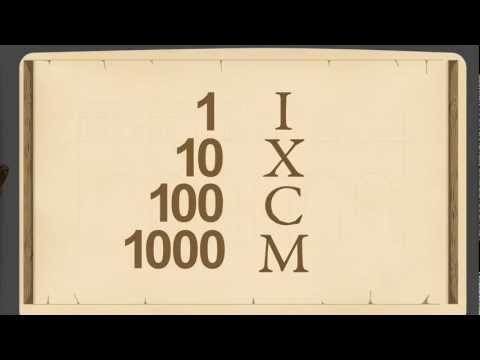Placeholder Image

字幕リスト動画再生

    動画が英語ではありませんか？
    字幕と単語
    A2 初級米

    代数2 - ローマ数字.符号-値と位置表記 (Pre-Algebra 2 - Roman Numerals: Sign-Value vs Positional Notation)

    00
    Chun Sang Suen が 2021 年 01 月 14 日 に投稿
    保存
    動画の中の単語

    equivalent

    US /ɪˈkwɪvələnt/

    ・

    UK /ɪˈkwɪvələnt/

    • adj.同等の；同義の
    • n.等価 : (効果 : 価値などが)同等のもの
    B1 中級TOEIC
    もっと見る
    pattern

    US /ˈpætən/

    ・

    UK /'pætn/

    • n. (c./u.)模範 : 見本；模様 : 柄；様式；規則性；型紙
    • v.t.模倣する；模様をつける
    A2 初級TOEIC
    もっと見る
    determine

    US /dɪˈtɚmɪn/

    ・

    UK /dɪ'tɜ:mɪn/

    • v.t.決定する；究明する；左右する；決意する
    A2 初級TOEIC
    もっと見る
    instance

    US /ˈɪnstəns/

    ・

    UK /'ɪnstəns/

    • n. (c./u.)例；発生；インスタンス
    • v.t.例に挙げる
    • phr.要請で
    A2 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary