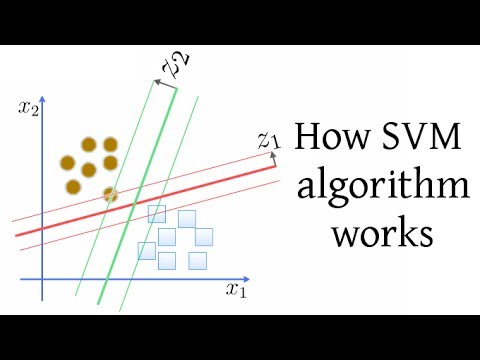
Placeholder Image

字幕リスト動画再生

    字幕と単語

    00
    保存
    動画の中の単語

    constant

    US /ˈkɑnstənt/

    ・

    UK /'kɒnstənt/

    • adj.不断の；一定の；忠実な
    • n.定数；定数
    A2 初級TOEIC
    もっと見る
    term

    US /tɚm/

    ・

    UK /tɜ:m/

    • n. (c./u.)条件；期間；学期；用語；関係；項；妊娠期間；任期
    • v.t.称する
    A1 初級TOEIC
    もっと見る
    scale

    US /skel/

    ・

    UK /skeɪl/

    • n. (c./u.)大きさや格など；うろこ；はかり；音階；規模
    • v.t./i.(縮尺比に従って)拡大する : 縮小する；登る；魚のうろこを取る
    A2 初級TOEIC
    もっと見る
    split

    US /splɪt/

    ・

    UK /splɪt/

    • adj.決別した；割れた；対立の
    • v.t./i.真っ直ぐに切って分けられる；割れる；対立する；分割する；公平に分ける
    • n. (c./u.)対立；分離
    A2 初級
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary