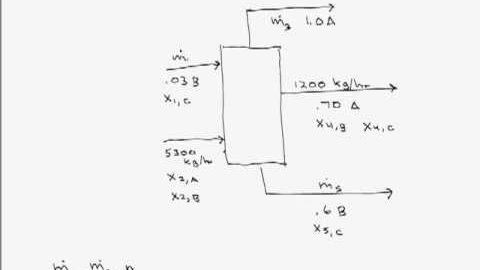
単一ユニットでの自由度分析 (Degree of Freedom Analysis on a Single Unit)
Jack が 2021 年 01 月 14 日 に投稿 
この条件に一致する単語はありません- v.t./i.出場する；計算する；思う；思う
- n.姿 : 体形；数字；人物像；図表；著名人；姿の輪郭；数字
- v.i.着く : 到着する；(郵便物が)～に届く；～という状態になる
- v.t./i.～に向かって進む : ～に同行する
US /kəmˈpliːtli/
・
UK /kəmˈpli:tli/
- n. (c./u.)休憩；静止；残りの部分；支え；休符
- v.t./i.休む；永眠する；傾ける；休養する；置く；残る
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除
