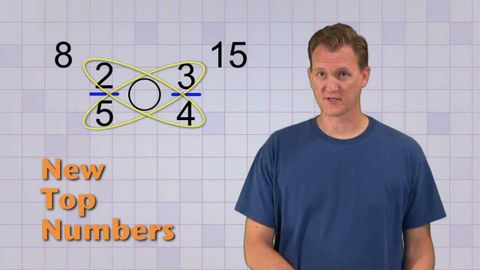
Placeholder Image

字幕リスト動画再生

    動画が英語ではありませんか？
    字幕と単語
    B1 中級米

    数学のアンチティクス - 分数の比較 (Math Antics - Comparing Fractions)

    00
    Yassion Liu が 2021 年 01 月 14 日 に投稿
    保存
    動画の中の単語

    practice

    US /ˈpræktɪs/

    ・

    UK /'præktɪs/

    • n.仕事；練習すること；慣習
    • v.t./i.開業；従う；練習する；実践する
    A2 初級TOEIC
    もっと見る
    pattern

    US /ˈpætən/

    ・

    UK /'pætn/

    • n. (c./u.)模範 : 見本；模様 : 柄；様式；規則性；型紙
    • v.t.模倣する；模様をつける
    A2 初級TOEIC
    もっと見る
    pretty

    US /ˈprɪti/

    ・

    UK /'prɪtɪ/

    • adj.かわいい；可愛い
    • adv.かなり；かなり
    • v.t.飾る : 美しくする
    • n.美人
    A1 初級TOEIC
    もっと見る
    trick

    US /trɪk/

    ・

    UK /trɪk/

    • v.t.だます；笑わす
    • n. (c./u.)トリック；腕の良いやり方；技
    • adj.迷わせる
    A2 初級
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary