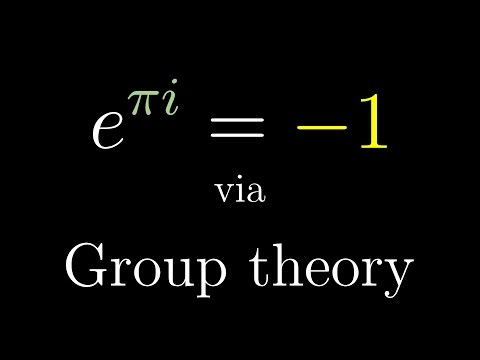字幕リスト動画再生

    動画が英語ではありませんか？
    字幕と単語

    00
    保存
    動画の中の単語

    specific

    US /spɪˈsɪfɪk/

    ・

    UK /spəˈsɪfɪk/

    • adj.明確な；特定の；明確な；特定の
    A2 初級
    もっと見る
    stretch

    US /strɛtʃ/

    ・

    UK /stretʃ/

    • v.t./i.ストレッチをする : 体を伸ばす；伸ばす : 張る : 広げる
    • n.ストレッチ : 体を伸ばすこと；一続きのもの；(一続きの)時間 : 期間
    A2 初級TOEIC
    もっと見る
    positive

    US /ˈpɑzɪtɪv/

    ・

    UK /ˈpɒzətɪv/

    • adj.肯定的な；確実な；電気のプラス極；よい；陽性の；楽観的な；正の；ポジ
    • n.ポジ
    A2 初級
    もっと見る
    flip

    US /flɪp/

    ・

    UK /flɪp/

    • v.t./i.空中で回転する；素早く(さっと)動く；スイッチの切り替えをする；ひっくり返す；転売する
    • n.回転；動かすこと；フリップ
    • adj.軽薄な
    B2 中上級
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary