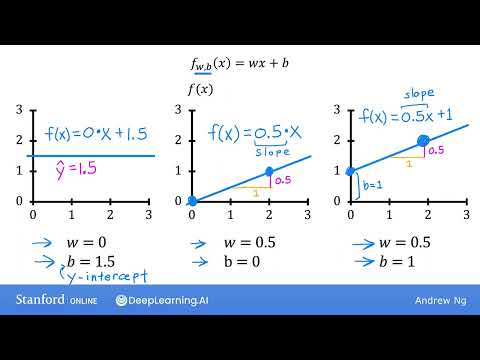
Placeholder Image

字幕リスト動画再生

    字幕と単語

    00
    保存
    動画の中の単語

    entire

    US /ɛnˈtaɪr/

    ・

    UK /ɪn'taɪə(r)/

    • adj.完全な；完全な；全縁の (植物学)
    A2 初級TOEIC
    もっと見る
    eventually

    US /ɪˈvɛntʃuəli/

    ・

    UK /ɪˈventʃuəli/

    • adv.最終的には；いつか
    A2 初級
    もっと見る
    constant

    US /ˈkɑnstənt/

    ・

    UK /'kɒnstənt/

    • adj.不断の；一定の；忠実な
    • n.定数；定数
    A2 初級TOEIC
    もっと見る
    expression

    US /ɪkˈsprɛʃən/

    ・

    UK /ɪk'spreʃn/

    • n. (c./u.)表現；語句；表情；式；表現；表現
    A2 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary