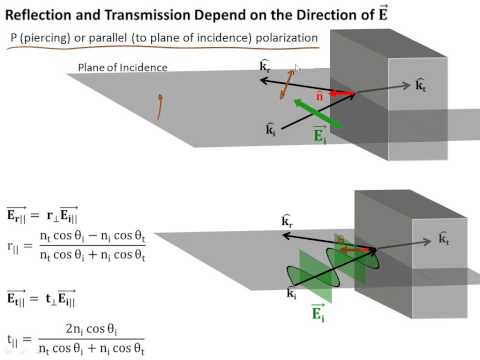
3.8 フレネル方程式 (3.8 Fresnel Equations)
kevin が 2024 年 10 月 07 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありません- v.t./i.突き刺す : 刺し込む;貼る : くっつける;とどまる;突き出す;我慢する
- n. (c.)棒
US /ɪˈsenʃəli/
・
UK /ɪˈsenʃəli/
- v.t.(人を騙すために)ふりをする : 装う;仮定する : 推測する;(責任 : 任務などを)負う : 引き受ける
US /ɪˈvɛntʃuəli/
・
UK /ɪˈventʃuəli/
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除