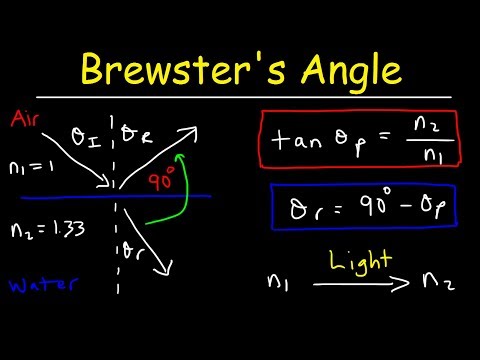
Placeholder Image

字幕リスト動画再生

AI 自動生成字幕
    動画が英語ではありませんか？
    字幕と単語
    AI 自動生成字幕
    C1 上級日本語米
    #屈折#角度#反射#光線#等しい#空気

    ブリュースター角、光の偏光、偏光角 - 物理学問題集 (Brewster's Angle, Polarization of Light, Polarizing Angle - Physics Problems)

    00
    kevin が 2024 年 10 月 02 日 に投稿
    保存
    動画の中の単語

    specific

    US /spɪˈsɪfɪk/

    ・

    UK /spəˈsɪfɪk/

    • adj.明確な；特定の；明確な；特定の
    A2 初級
    もっと見る
    equivalent

    US /ɪˈkwɪvələnt/

    ・

    UK /ɪˈkwɪvələnt/

    • adj.同等の；同義の
    • n.等価 : (効果 : 価値などが)同等のもの
    B1 中級TOEIC
    もっと見る
    approach

    US /əˈprəʊtʃ/

    ・

    UK /ə'prəʊtʃ/

    • v.t./i.近づく；話を持ちかける
    • n. (c./u.)目的に近づく方法 : 道；交渉しようとして人に近づくこと；取り組み方 : 扱い方
    A2 初級TOEIC
    もっと見る
    material

    US /məˈtɪriəl/

    ・

    UK /məˈtɪəriəl/

    • n. (c./u.)衣料；原材料；原料
    • adj.関連な,重要な；世俗的な : 物質的な : 物質でできた
    A2 初級
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary