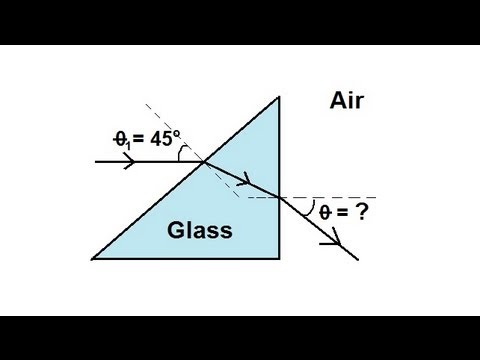
物理 52 屈折とスネルの法則(11の3)プリズムを通る光線 (Physics 52 Refraction and Snell's Law (3 of 11) Light Ray Through A Prism)
kevin が 2024 年 10 月 02 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありません- v.t.(人を騙すために)ふりをする : 装う;仮定する : 推測する;(責任 : 任務などを)負う : 引き受ける
- v.t./i.出場する;計算する;思う;思う
- n.姿 : 体形;数字;人物像;図表;著名人;姿の輪郭;数字
US /ˈriəˌlaɪz/
・
UK /'ri:əlaɪz/
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除