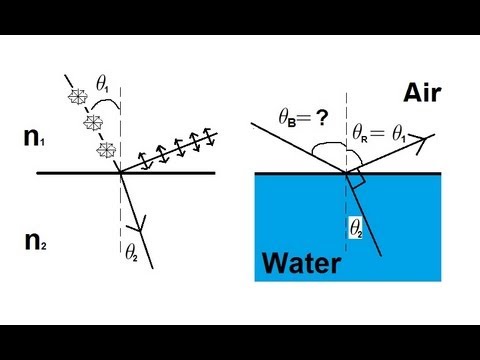
物理 53 偏光(5/5) ブリュースター角 (Physics 53 Polarization (5 of 5) Brewster's Angle)
kevin が 2024 年 10 月 02 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありません- v.t.(人を騙すために)ふりをする : 装う;仮定する : 推測する;(責任 : 任務などを)負う : 引き受ける
US /fɪˈnɑməˌnɑn, -nən/
・
UK /fə'nɒmɪnən/
- n. (c./u.)条件;期間;学期;用語;関係;項;妊娠期間;任期
- v.t.称する
US /ˈriəˌlaɪz/
・
UK /'ri:əlaɪz/
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除