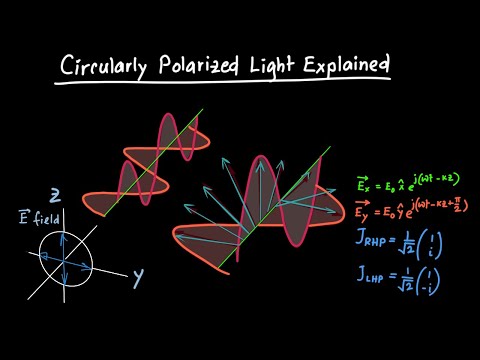
円偏光の説明 (Circularly Polarized Light Explained)
kevin が 2024 年 09 月 21 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありません- v.t./i.突き刺す : 刺し込む;貼る : くっつける;とどまる;突き出す;我慢する
- n. (c.)棒
- v.t.(人を騙すために)ふりをする : 装う;仮定する : 推測する;(責任 : 任務などを)負う : 引き受ける
US /ˈpɪriəd/
・
UK /ˈpɪəriəd/
- n. (c./u.)期間 : 時代;強調;終止符;生理;授業時間 : 時限
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除