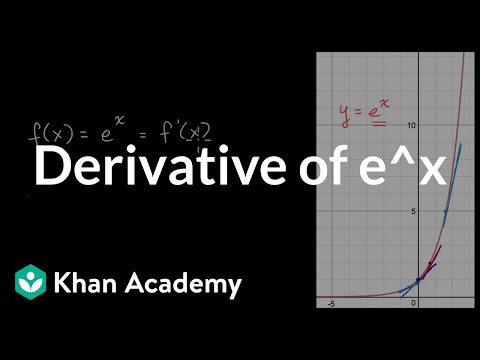
Derivative of __ | Advanced derivatives | AP Calculus AB | Khan Academy
yukang920108 が 2022 年 07 月 12 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありませんUS /ɪkˈsprɛʃən/
・
UK /ɪk'spreʃn/
- n. (c./u.)表現;語句;表情;式;表現;表現
US /ˈfæsəˌnetɪŋ/
・
UK /ˈfæsɪneɪtɪŋ/
- v.t.魅惑的な;(視線で)捕らえる
- adj.魅惑的な
- n. (u.)魅力
US /ˈriəˌlaɪz/
・
UK /'ri:əlaɪz/
US /ˌri:ɪnˈfɔ:rs/
・
UK /ˌri:ɪnˈfɔ:s/
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除