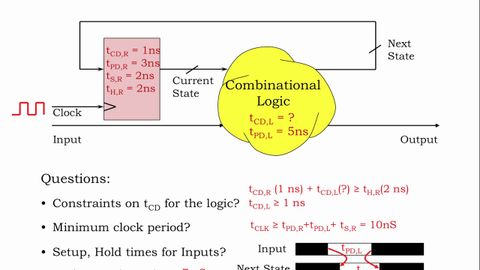
5.2.6 タイミング例 (5.2.6 Timing Example)
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありませんUS /ˈdɪsəplɪn/
・
UK /'dɪsəplɪn/
- n. (c./u.)規律;訓練;学科;懲罰;自制
- v.t.訓練する;懲罰を与える
- v.t./i.出場する;計算する;思う;思う
- n.姿 : 体形;数字;人物像;図表;著名人;姿の輪郭;数字
US /ˈpɪriəd/
・
UK /ˈpɪəriəd/
- n. (c./u.)期間 : 時代;強調;終止符;生理;授業時間 : 時限
US /daiˈnæmik/
・
UK /daɪˈnæmɪk/
- adj.行動的な : 活動的な : 生き生きした : 活力に満ちた
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除