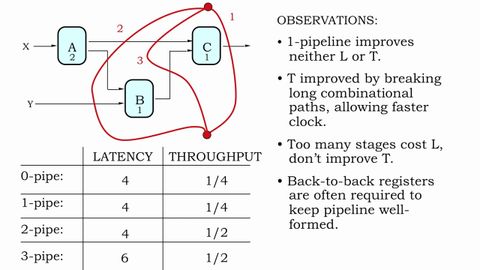
Placeholder Image

字幕リスト動画再生

    動画が英語ではありませんか？
    字幕と単語
    B2 中上級

    7.2.3 パイプラインの方法論 (7.2.3 Pipelining Methodology)

    00
    林宜悉 が 2021 年 01 月 14 日 に投稿
    保存
    動画の中の単語

    assume

    US /əˈsum/

    ・

    UK /ə'sju:m/

    • v.t.(人を騙すために)ふりをする : 装う；仮定する : 推測する；(責任 : 任務などを)負う : 引き受ける
    A2 初級TOEIC
    もっと見る
    process

    US /ˈprɑsˌɛs, ˈproˌsɛs/

    ・

    UK /prə'ses/

    • v.t.(コンピュータの)データを処理する；処理する；処理する；一連の工程を経る；加工する : 加工処理する；理解する
    • n. (c./u.)手続き；一連の行為；方法；訴訟手続き；プロセス (コンピューター)
    A2 初級TOEIC
    もっと見る
    strategy

    US /ˈstrætədʒi/

    ・

    UK /'strætədʒɪ/

    • n. (c./u.)戦略；戦略
    A2 初級TOEIC
    もっと見る
    technique

    US /tɛkˈnik/

    ・

    UK /tekˈni:k/

    • n. (c./u.)技術 : 技巧 : テクニック；技能；技法
    A2 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary