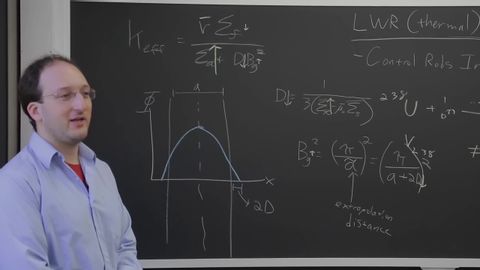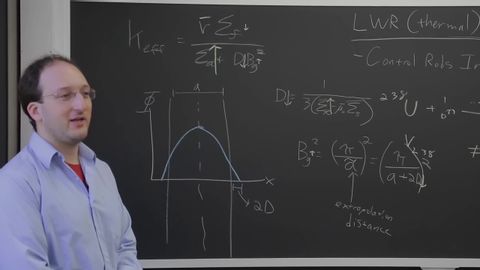Placeholder Image

字幕リスト動画再生

    動画が英語ではありませんか？
    字幕と単語
    B2 中上級

    24.過渡現象、フィードバック、時間依存性中性子 (24. Transients, Feedback, and Time-Dependent Neutronics)

    00
    林宜悉 が 2021 年 01 月 14 日 に投稿
    保存
    動画の中の単語

    critical

    US /ˈkrɪtɪkəl/

    ・

    UK /ˈkrɪtɪkl/

    • adj.批判的な；重大な；批評の；批判的な；重篤な
    A2 初級
    もっと見る
    material

    US /məˈtɪriəl/

    ・

    UK /məˈtɪəriəl/

    • n. (c./u.)衣料；原材料；原料
    • adj.関連な,重要な；世俗的な : 物質的な : 物質でできた
    A2 初級
    もっと見る
    period

    US /ˈpɪriəd/

    ・

    UK /ˈpɪəriəd/

    • n. (c./u.)期間 : 時代；強調；終止符；生理；授業時間 : 時限
    A1 初級TOEIC
    もっと見る
    term

    US /tɚm/

    ・

    UK /tɜ:m/

    • n. (c./u.)条件；期間；学期；用語；関係；項；妊娠期間；任期
    • v.t.称する
    A1 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary