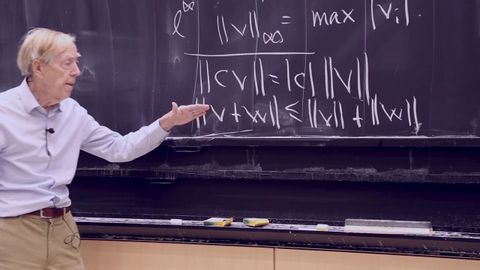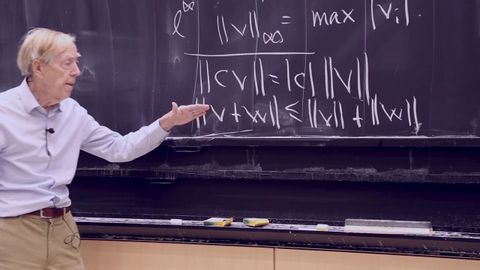7.エッカート・ヤングAに最も近いランクkの行列 (7. Eckart-Young: The Closest Rank k Matrix to A)
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありません- n. (c./u.)集まり;仲間
- v.t.まとまる
- v.t./i.束ねられる
US /ˈævərɪdʒ, ˈævrɪdʒ/
・
UK /'ævərɪdʒ/
- n. (c./u.)平均
- v.t.平均する
- adj.典型的な : 普通の : ありふれた : 普段の
US /ˈnɛɡətɪv/
・
UK /'neɡətɪv/
- n.マイナスの電極;否定文の;「いや」という返事;写真や映画のネガ
- adj.嫌な;負の数の;悲観的な;否定的;陰性の;負の
US /ˈɔdiəns/
・
UK /ˈɔ:diəns/
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除