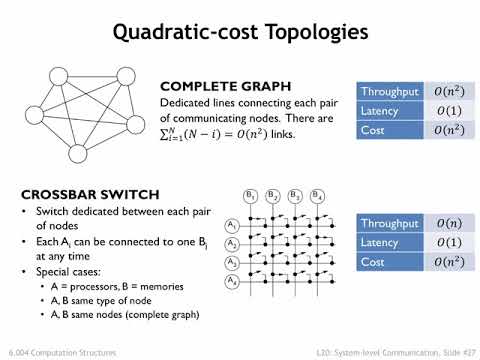
Placeholder Image

字幕リスト動画再生

    動画が英語ではありませんか？
    字幕と単語
    B2 中上級

    20.2.6 通信トポロジ (20.2.6 Communication Topologies)

    00
    林宜悉 が 2021 年 01 月 14 日 に投稿
    保存
    動画の中の単語

    assume

    US /əˈsum/

    ・

    UK /ə'sju:m/

    • v.t.(人を騙すために)ふりをする : 装う；仮定する : 推測する；(責任 : 任務などを)負う : 引き受ける
    A2 初級TOEIC
    もっと見る
    process

    US /ˈprɑsˌɛs, ˈproˌsɛs/

    ・

    UK /prə'ses/

    • v.t.(コンピュータの)データを処理する；処理する；処理する；一連の工程を経る；加工する : 加工処理する；理解する
    • n. (c./u.)手続き；一連の行為；方法；訴訟手続き；プロセス (コンピューター)
    A2 初級TOEIC
    もっと見る
    sophisticated

    US /səˈfɪstɪˌketɪd/

    ・

    UK /səˈfɪstɪkeɪtɪd/

    • adj.話をより複雑にする；洗練された
    • v.t.洗練させた
    B1 中級TOEIC
    もっと見る
    alternative

    US /ɔlˈtɚnətɪv, æl-/

    ・

    UK /ɔ:lˈtɜ:nətɪv/

    • n. (c.)選択肢 : 代替案
    • adj.代替案
    A2 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary