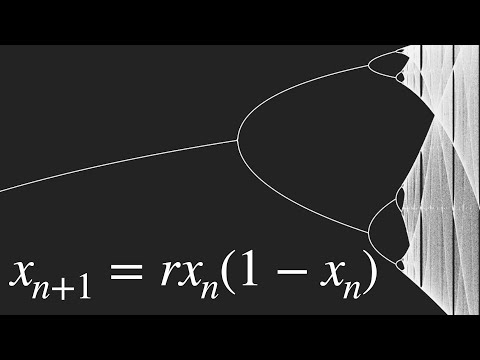
この方程式で世界の見え方が変わる(ロジスティックマップ (This equation will change how you see the world (the logistic map))
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありませんUS /ɪˈvɛntʃuəli/
・
UK /ɪˈventʃuəli/
US /ɪnˈkrɛdəblɪ/
・
UK /ɪnˈkredəbli/
- adv.信じられないことに;信じられないほど;信じられないほど;驚くほど
US /ˈkɑnstənt/
・
UK /'kɒnstənt/
US /ˈpɪriəd/
・
UK /ˈpɪəriəd/
- n. (c./u.)期間 : 時代;強調;終止符;生理;授業時間 : 時限
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除