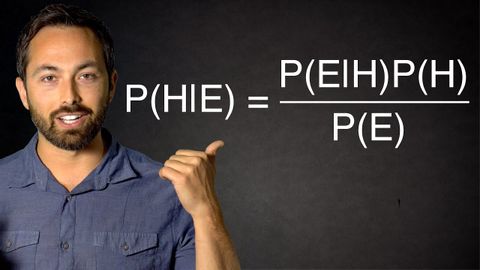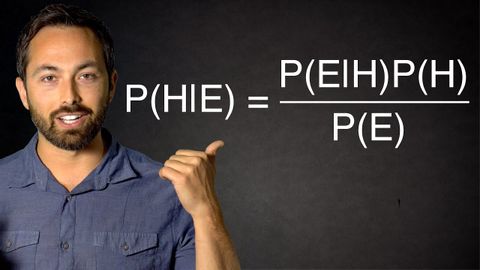ベイズの罠 (The Bayesian Trap)
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありません- v.t.(報いや賞などを受けるに)値する : ~の価値がある
US /ˈɛvɪdəns/
・
UK /'evɪdəns/
US /dɪˈtɚmɪn/
・
UK /dɪ'tɜ:mɪn/
US /ˈpɑzɪtɪv/
・
UK /ˈpɒzətɪv/
- adj.肯定的な;確実な;電気のプラス極;よい;陽性の;楽観的な;正の;ポジ
- n.ポジ
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除