字幕と単語
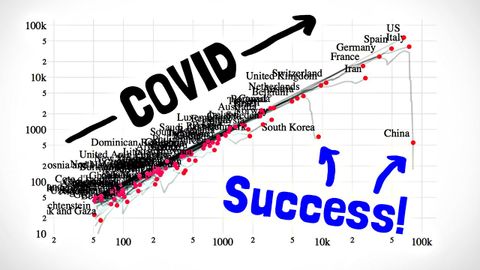
COVID-19に勝っているかどうかの見分け方 (How To Tell If We're Beating COVID-19)
00
林宜悉 が 2021 年 01 月 14 日 に投稿保存
動画の中の単語
scale
US /skel/
・
UK /skeɪl/
- n. (c./u.)大きさや格など;うろこ;はかり;音階;規模
- v.t./i.(縮尺比に従って)拡大する : 縮小する;登る;魚のうろこを取る
A2 初級TOEIC
もっと見る エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除
