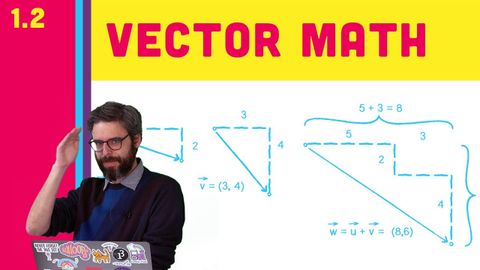
1.2 ベクトル数学 - コードの性質 (1.2 Vector Math - The Nature of Code)
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありませんUS /ˈʌltəmɪtli/
・
UK /ˈʌltɪmətli/
US /ɪˈkwɪvələnt/
・
UK /ɪˈkwɪvələnt/
- adj.同等の;同義の
- n.等価 : (効果 : 価値などが)同等のもの
- v.t./i.出場する;計算する;思う;思う
- n.姿 : 体形;数字;人物像;図表;著名人;姿の輪郭;数字
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除