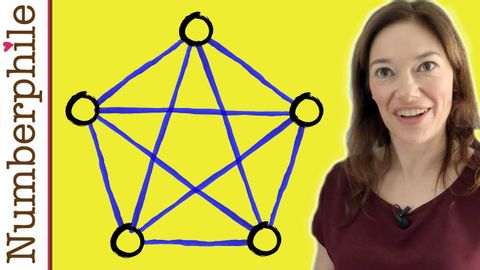
平面グラフ - Numberphile (Planar Graphs - Numberphile)
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありませんUS /ɪnˈkrɛdəbəl/
・
UK /ɪnˈkredəbl/
- adj.信じられない;すばらしい;信じられない;信じられない
- n. (c./u.)集まり;仲間
- v.t.まとまる
- v.t./i.束ねられる
- n. (c./u.)散らかっていること : 乱雑さ : 汚らしさ;問題;食べ物;食堂
- v.t.(物を)乱雑にする : ごちゃごちゃにする
US /ˈprɑpəti/
・
UK /'prɒpətɪ/
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除