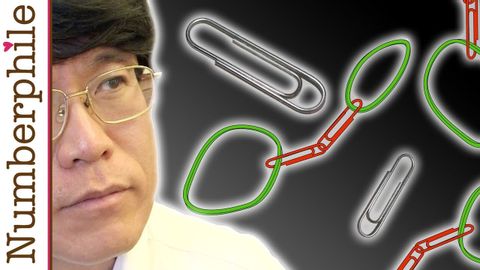
難解な紙クリップ - Numberphile (Perplexing Paperclips - Numberphile)
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありません- v.t./i.突き刺す : 刺し込む;貼る : くっつける;とどまる;突き出す;我慢する
- n. (c.)棒
US /ɪn'gedʒ/
・
UK /ɪn'ɡeɪdʒ/
- v.t.武力によって衝突する;雇用する;人の興味を引く;従事する;かみ合う;約束する
US /ɪkˈspɛrəmənt/
・
UK /ɪk'sperɪmənt/
- n. (c./u.)実験;試み
- v.t./i.実験をする;試みる
US /fəˈmɪljɚ/
・
UK /fəˈmɪliə(r)/
- adj.よく知られた;精通;親しげな
- n.親友;使い魔
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除