字幕と単語
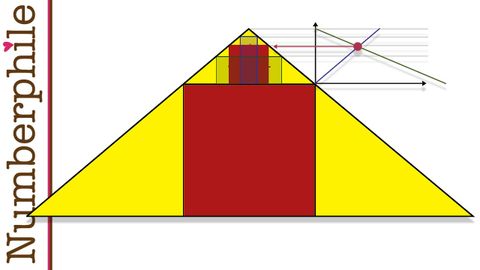
三角形の中に正方形を描く3つの方法 - Numberphile (3 Ways to Draw Squares Inside Triangles - Numberphile)
00
林宜悉 が 2021 年 01 月 14 日 に投稿保存
動画の中の単語
straight
US /stret/
・
UK /streɪt/
- adj.異性愛者;異性愛の;正直で直接的;真っ直ぐな;きちんとした
- adv.率直に;まっすぐに;すぐに
- n.異性愛者
- v.t./i.まっすぐにする
A2 初級TOEIC
もっと見る エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除
