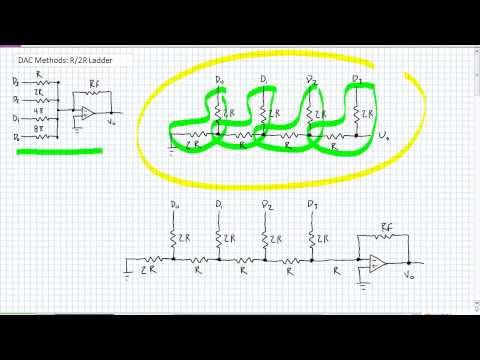
DACメソッド R2Rラダー (DAC Methods R2R Ladder)
jmkuoa が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありませんUS /pɚˈspɛktɪv/
・
UK /pə'spektɪv/
US /ɪˈkwɪvələnt/
・
UK /ɪˈkwɪvələnt/
- adj.同等の;同義の
- n.等価 : (効果 : 価値などが)同等のもの
US /sɪɡˈnɪfɪkənt/
・
UK /sɪgˈnɪfɪkənt/
US /ˈbesɪkəli,-kli/
・
UK /ˈbeɪsɪkli/
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除