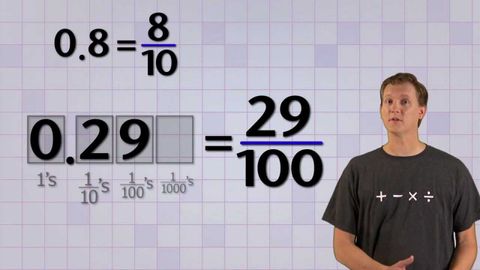
字幕と単語
数学アンチックス - ベース10の分数の変換 (Math Antics - Converting Base-10 Fractions)
00
Yassion Liu が 2021 年 01 月 14 日 に投稿保存
動画の中の単語
time
US /taɪm/
・
UK /taɪm/
- n. (u.)(音楽の)拍子 : テンポ;(時計が指し示す)時刻 : 時間;時間;(ある出来事が起きる)時 : 時点;時;時代 : 時期;時間;所要時間
- v.t.(音楽の)リズムをとる;(~するのに)ふさわしい時を選ぶ;時間を計る;(出来事の最適な時間や時期を)決める
A1 初級TOEIC
もっと見る エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除
