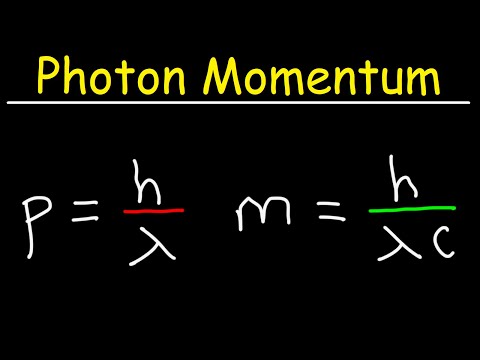
Placeholder Image

字幕リスト動画再生

AI 自動生成字幕
    動画が英語ではありませんか？
    字幕と単語
    AI 自動生成字幕
    B2 中上級日本語米
    #光子#波長#質量#運動#定数#プランク

    光子運動量と有効質量 (Photon Momentum and Effective Mass)

    00
    kevin が 2024 年 10 月 02 日 に投稿
    保存
    動画の中の単語

    constant

    US /ˈkɑnstənt/

    ・

    UK /'kɒnstənt/

    • adj.不断の；一定の；忠実な
    • n.定数；定数
    A2 初級TOEIC
    もっと見る
    negative

    US /ˈnɛɡətɪv/

    ・

    UK /'neɡətɪv/

    • n.マイナスの電極；否定文の；「いや」という返事；写真や映画のネガ
    • adj.嫌な；負の数の；悲観的な；否定的；陰性の；負の
    A2 初級
    もっと見る
    effective

    US /ɪˈfɛktɪv/

    ・

    UK /ɪˈfektɪv/

    • adj.効果的な；有効な；有能な；事実上の
    A1 初級TOEIC
    もっと見る
    treat

    US /trit/

    ・

    UK /tri:t/

    • v.t.おごる；治療する；扱う；処理する
    • n. (c./u.)おごり；珍味；ご褒美
    A1 初級TOEIC
    もっと見る
    エネルギーを使用
    すべての単語を解除
    発音・解説・フィルター機能を解除
    energy point vocabulary