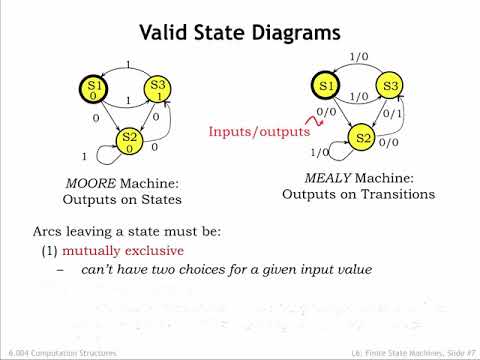
6.2.2 状態遷移図 (6.2.2 State Transition Diagrams)
林宜悉 が 2021 年 01 月 14 日 に投稿  この条件に一致する単語はありません
この条件に一致する単語はありませんUS /ˈdɪsəplɪn/
・
UK /'dɪsəplɪn/
- n. (c./u.)規律;訓練;学科;懲罰;自制
- v.t.訓練する;懲罰を与える
US /əˈprəʊtʃ/
・
UK /ə'prəʊtʃ/
- v.t./i.近づく;話を持ちかける
- n. (c./u.)目的に近づく方法 : 道;交渉しようとして人に近づくこと;取り組み方 : 扱い方
US /ˈtrɪɡɚ/
・
UK /'trɪɡə(r)/
- n.引き金;事を開始する装置;きっかけ;トラウマの引き金;トリガー (電子工学);トリガー (コンピュータ);トリガー (釣り)
- v.t.引き起こす;引き起こす;反射を引き起こす
US /ɪkˈsklusɪv/
・
UK /ɪk'sklu:sɪv/
- adj.(裕福層)限定の;排他的な;独占記事;〜を含まない;排他的
エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除