字幕と単語
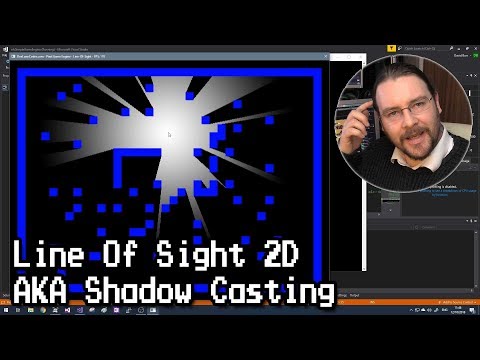
2Dでのラインオブサイトまたはシャドウキャスティング (Line Of Sight or Shadow Casting in 2D)
00
林宜悉 が 2021 年 01 月 14 日 に投稿保存
動画の中の単語
routine
US /ruˈtin/
・
UK /ru:ˈti:n/
- adj.日課の;繰り返しの;決まりきった
- n. (c./u.)日課 : 習慣となっているもの;芝居;単調;手順
A2 初級TOEIC
もっと見る エネルギーを使用
すべての単語を解除
発音・解説・フィルター機能を解除
